关键词匹配算法调研

在负责的规则系统中有很大一部分的规则是对用户输入的文本做关键词的匹配。整个关键词功能中有几个概念:

• 匹配词：如果目标文本中存在匹配词，就认为规则是命中的。
• 排除词：如果目标文本中存在排除词，就认为规则是不命中的。

其中排除词的优先于匹配词的。另外还有一个组合概念，就是只有两个或者以上的关键词命中的时候才算命中，这个在排除词和匹配词中都会有。

原本的实现是通过正则表达式的方式实现的。针对每个词都创建一个java.regex.Pattern，再对目标字符串进行匹配。

最新一个新业务提出了需要支持一个规则中最多包含500个关键词，这个长度比我们目前现有规则中最长的关键长了至少10倍。所以现有的实现能否满足整体的性能要求存在疑虑。

调研了现在常用的字符串匹配算法，发现AC多模匹配算法比较适合我们的场景。

AC多模式匹配算法

AC多模算法通过将多个关键词构造成一个有限状态机，然后再用状态机来处理输入文本。通过AC算法可以在O(n)时间内完成匹配，而且与关键词的长度无关。

AC算法的主要步骤有:

• 为所有的关键词构造一个前缀树结构
• 针对前缀树中的每个节点计算出匹配失败后的跳转以及节点的输出
• 对目标串进行模式匹配

其中在完成前两步的过程需要用到三个函数：

• goto : 根据当前状态s以及输入字符a 计算出下一个状态s' = goto(s, a)
• fail : 当前上一步goto函数的结果为fail时，需要使用该函数计算出下一个状态
• output : 当goto函数达到某个状态时，该状态的输出内容

构造Goto Function

假设现在有一组关键词{he, she, his, hers}，那么通过AC算法构造出来的步骤为:

1. 树的根节点为0。

2. 输入 he 的到如下图。其中：goto(0, h)=1 goto(1,e) = 2，同时状态0到状态2得到了关键词he，记录output(2) = [he]

1. 输入 she。

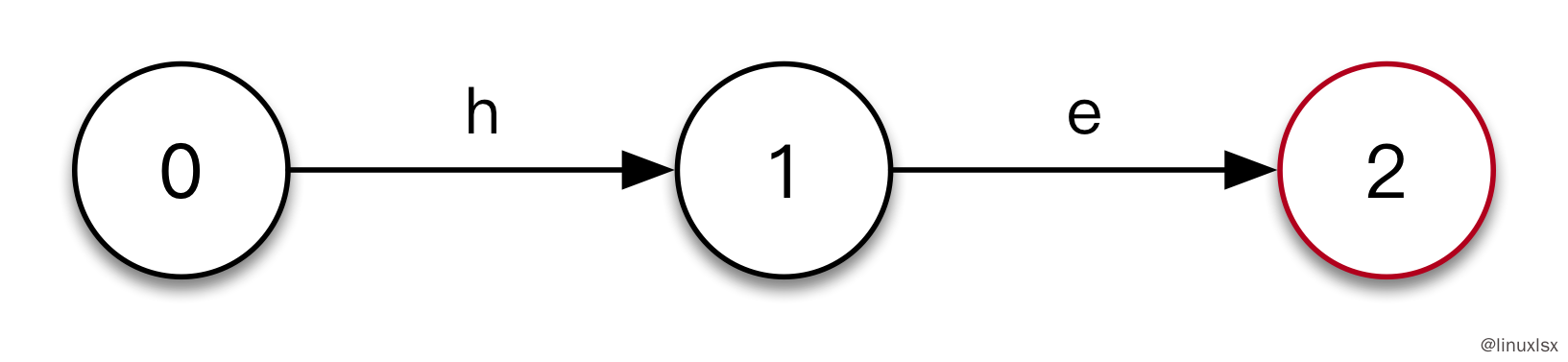
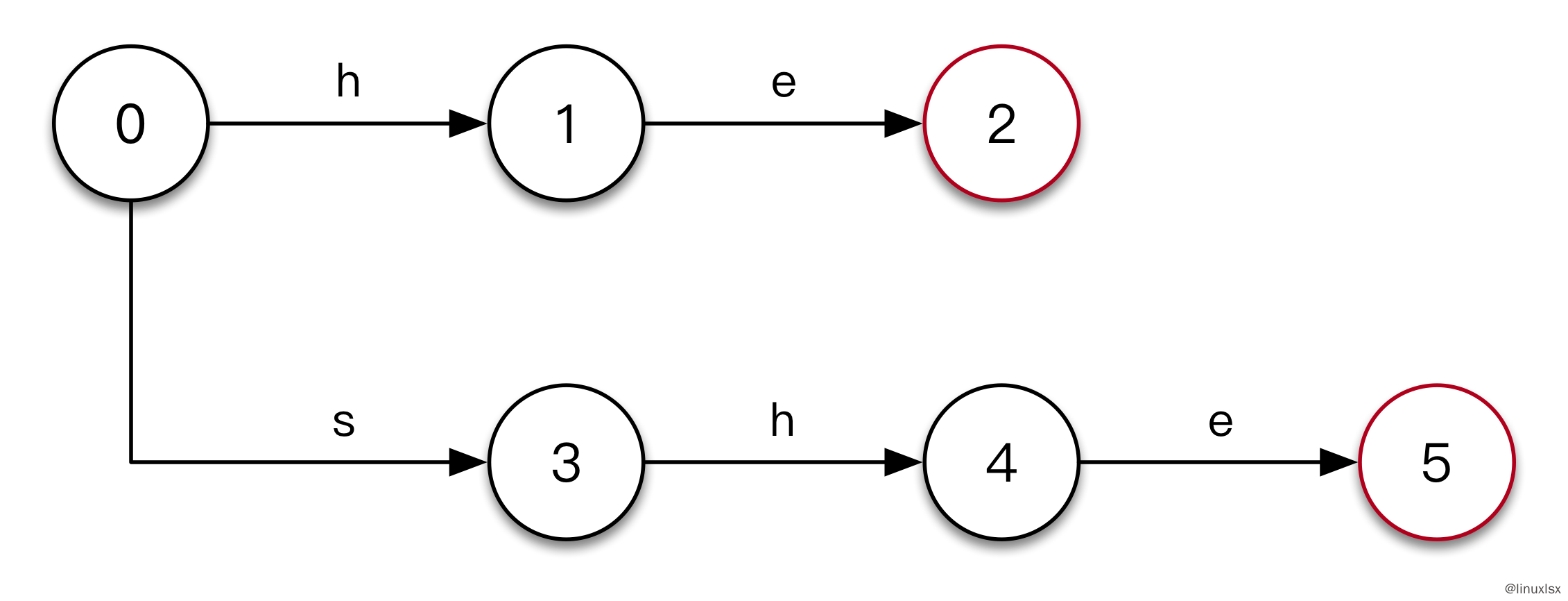
1. 输入 his。因为已经存在了h的状态转移，所以不需要从根节点开始，直接从节点1开始。

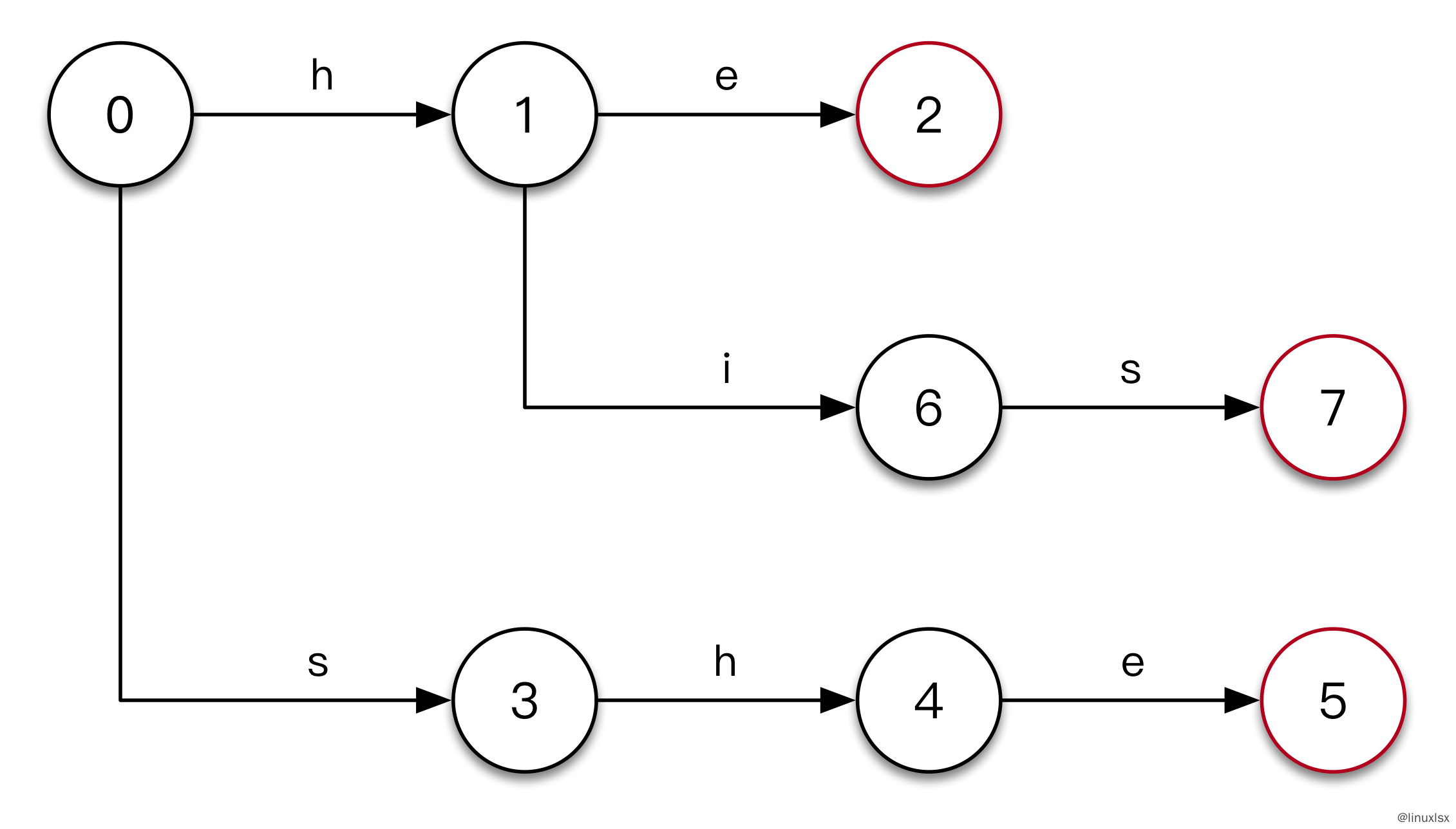
1. 输入 hers。得到最终的树。

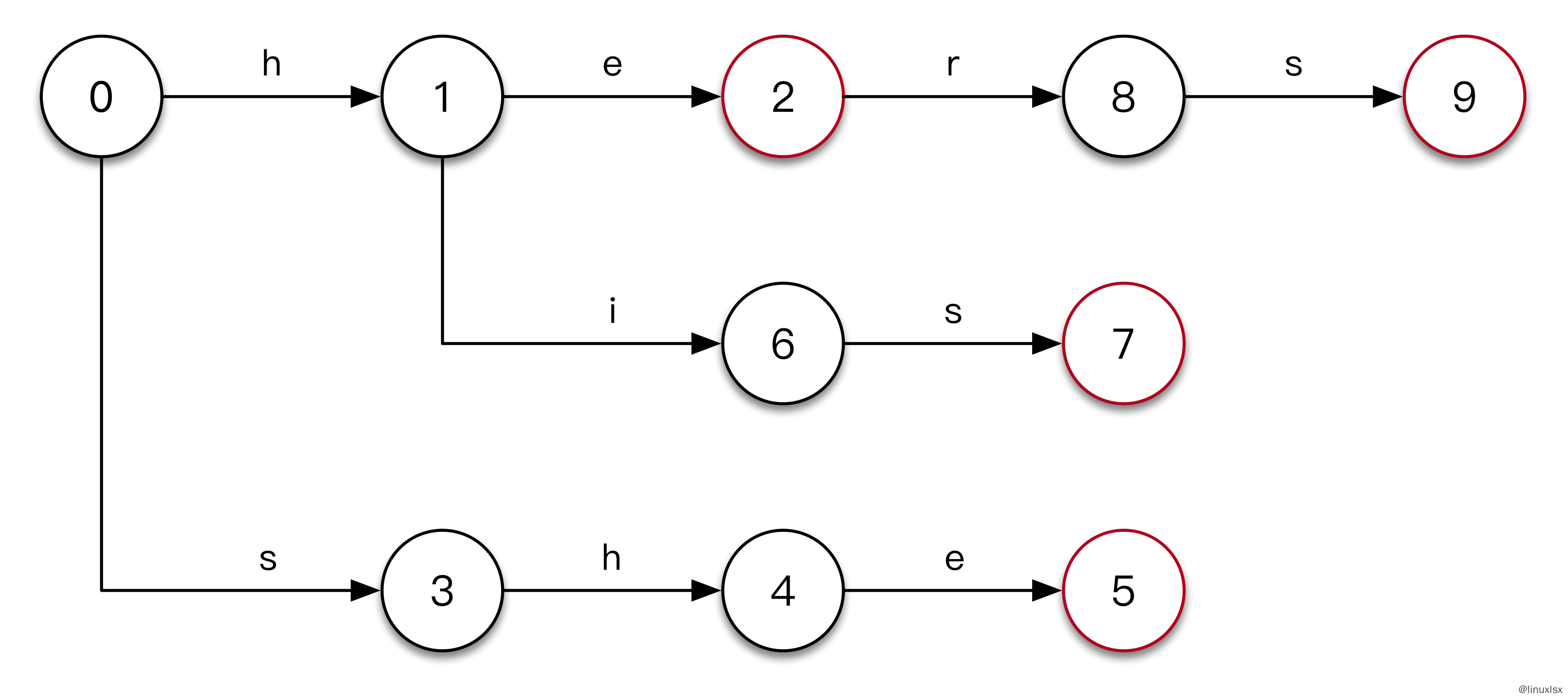
构造Fail Function

在Goto function构建完成以后，就需要构建Fail Function。首先要引入depth的概念: depth表示在goto树中从根节点到节点s的最短路径。针对上述的例子来说：节点1，3的depth为1, 节点2，4，6的depth为2，节点5，7，8的depth为3，节点9的depth为4。

计算失效函数的思路是这样的：首先计算深度为1 的状态的失效函数值，然后是深度为2的，以此类推，直到所有状态的失效函数值都被计算出。同时，算法规定所有深度为1的状态的fail值为0，假设所有深度小于d的状态的fail值都已经计算出，考虑每个深度为d-1的状态r，基于这些已经被计算出的深度为d-1的fail值，是可以得到深度为d的fail值的。

假设正在计算depth=d的节点s的f(s)，那么需要对depth=(d-1)的节点r执行以下的流程:

• 对于所有的字符a，如果goto(r,a) = fail，那么什么也不做
• 如果goto(r,a) == s，我们记state = f(r)，执行state = f(state)零次或者若干次，直到使得goto(state,a) != fail，因为goto(0,a) != fail，所以这个状态是一定存在的。
• 记fail(s) = goto(state,a)。

那么针对该案例的来讲，计算过程如下:

1
2
3
4
5
6
7
8
9
10
11

1. f(1),f(3)=0，因为这两个点depth=1
2. 第二层：
    2.1 节点2：state = f(1) = 0 => g(0, e) = 0 => f(2) = 0
    2.2 节点6：state = f(1) = 0 => g(0, i) = 0 => f(6) = 0       
    2.3 节点4：state = f(3) = 0 => g(0, h) = 1 => f(4) = 1
3. 第三层：
    3.1 节点8：state = f(2) = 0 => g(0, r) = 0 => f(8) = 0       
    3.2 节点7：state = f(6) = 0 => g(0, s) = 3 => f(7) = 3
    3.3 节点5：state = f(4) = 1 => g(1, e) = 2 => f(5) = 2
4. 第四层：
    4.1 节点9：state = f(8) = 0 => g(0, s) = 3 => f(9) = 3

整体的Fail Function结果表为:

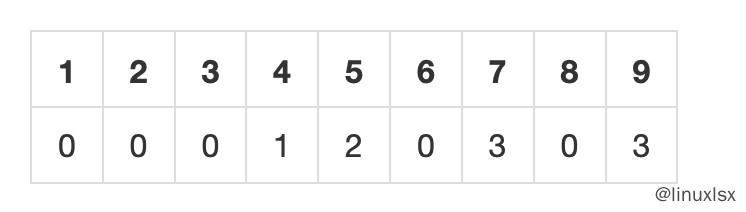
增加了Fail Function的图为:

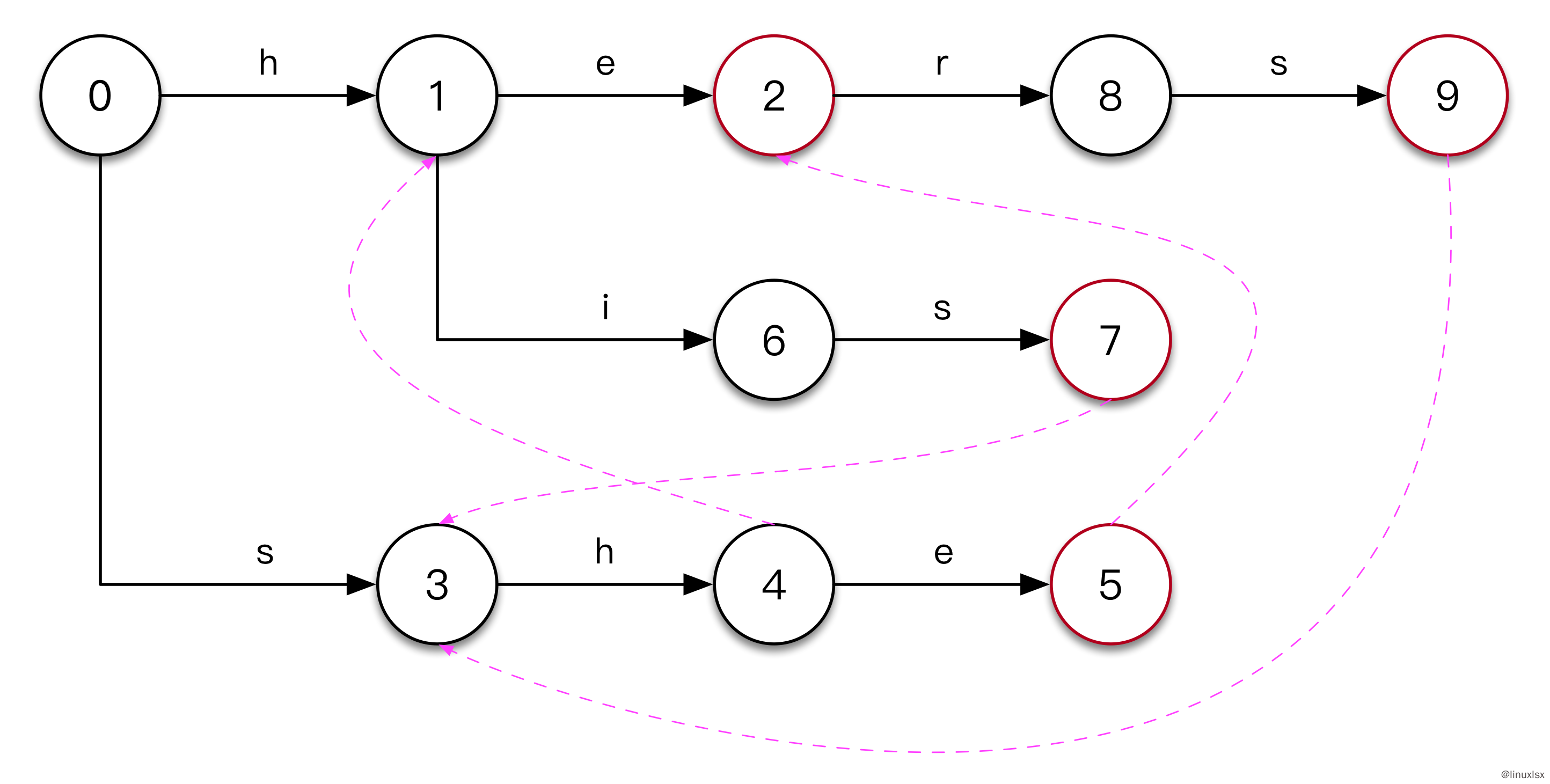
构造Output函数

Output函数结果的构造在以上两步中一起完成。首先在构造goto函数的时候，会把关键词增加到改关键词最后一个字符关联的节点的输出中。所以在第一步后：节点2，5，7，9的output中会有对应的关键词。

然后在构造Fail Function中，如果output(f(s)) != null，则把output(f(s))的结果添加到output(s)中。

以下是最终的结果表:

文本匹配

经过上述的步骤完成构建以后，就可以进行文本匹配了。只需要对文本从前到后进行一次遍历就可以，不需要进行回溯。

该过程的伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12

begin
    state <- 0
    for i <- until n do
        begin
            while g(state, ai) == fail do state <- f(state)
            state <- g(state, ai)
            if output(state) != empty then
                begin
                    print output(state)
                end
        end
end

性能比对

待匹配文本有三种长度: 50个字符，9Kb，36Kb 关键词数量(不存在匹配词): 1个，10个，50个(存在多分组) 关键词数量(存在一个匹配词，在最前): 1个，10个，50个(存在多分组) 关键词数量(存在一个匹配词，在中间): 1个，10个，50个(存在多分组) 关键词数量(存在一个匹配词，在最后): 1个，10个，50个(存在多分组) 关键词数量500。

测试通过JMH框架，单线程执行，预热3次，迭代6次，取平均值，单位为opt/s。

如下图可以看到:

• 1个关键词的时候，原实现性能比AC性能要好。但是AC算法和原实现也没有数量级的差异。
• 当关键词数量超过10个的时候，AC算法的性能要比原实现好。命中词在最前面算是一个特例，对于原实现来说相当于只有一个词的情况。 当然在短文本的情况下，原实现的绝对数量还是可以的，50个关键词短文本可以达到 18w次/每秒。
• 500词的情况下，AC算法有绝对的优势。

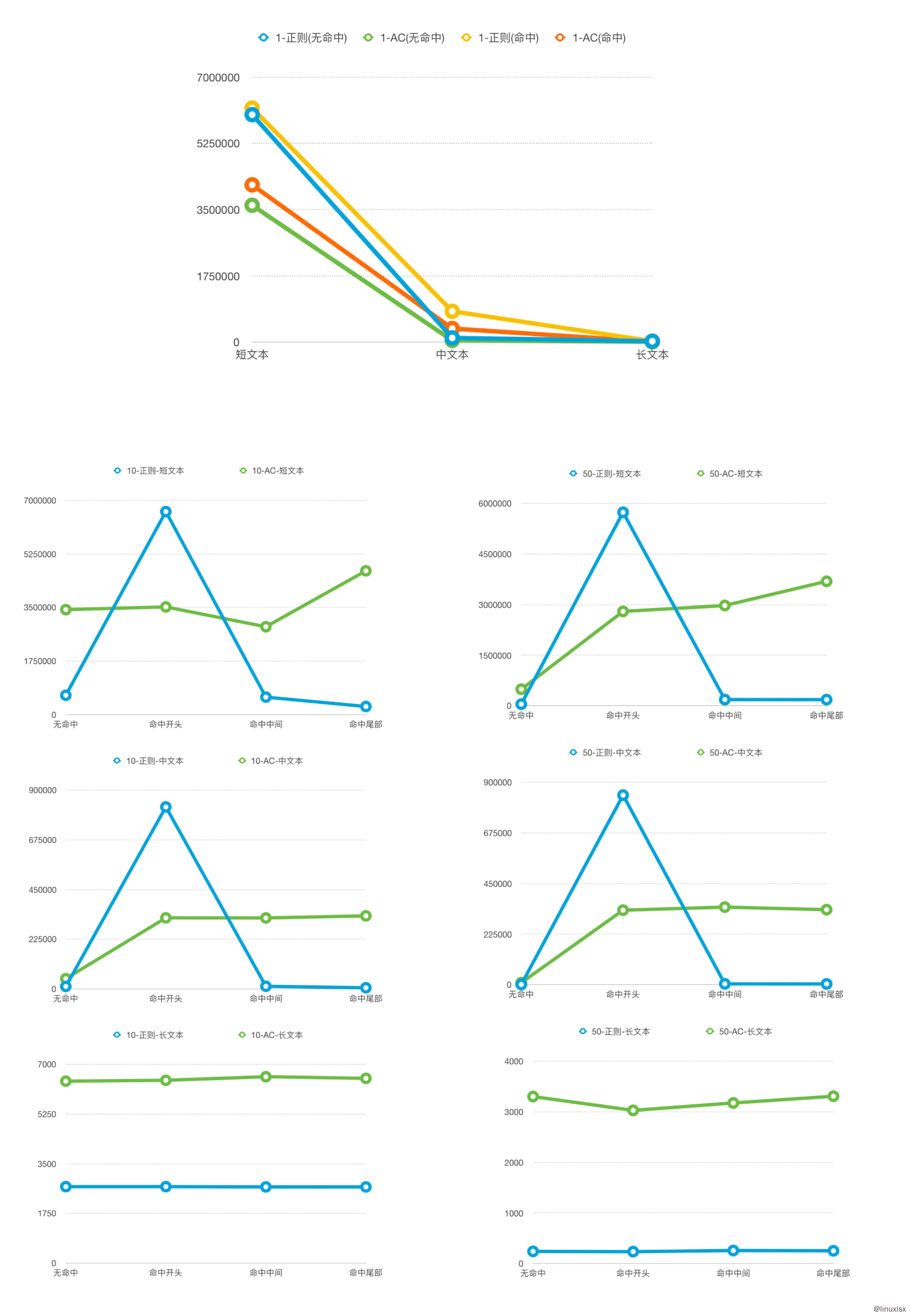
500个关键词性能表(AC的长串性能比较高，可能是内容中的命中词比较靠前)，可以看到即使在500词的情况下，性能仍然保持在高水平。:

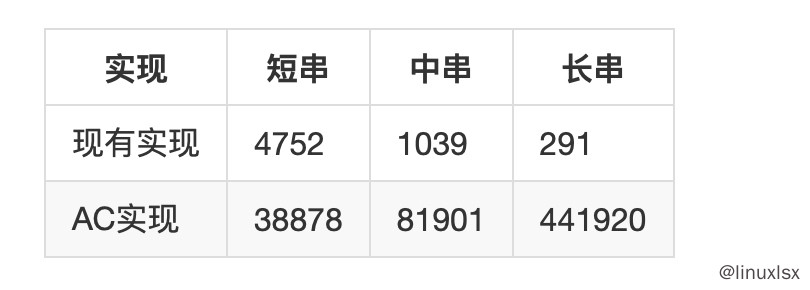
总结

AC算法在关键词比较多的情况下性能比原实现有非常明显的优势，特别是在中长文本的情况下。所以对于新需求可以通过AC算法实现，通用情况下也可以考虑使用AC算法实现替换掉。

参考

AC算法论文

AC算法在美团上单系统的应用